교란 해소
인과관계는 세상을 이해하는 기본적인 개념이기 때문에 직관적으로 이해할 수 있습니다. 하지만 직관과 데이터 분석은 교란 때문에 잘못된 방향으로 흘러갈 수 있습니다. 두 관심 변수의 공동 요인을 제대로 이해하지 못하면 상황을 잘못 해석하게 되고 관심 요인에 대한 회귀 계수는 편향됩니다. 따라서 어떤 변수를 포함하고 어떤 변수를 포함하지 않을지 결정하는 것은 데이터 분석 또는 더 나아가 인과적 사고방식의 교란을 해소하는 가장 중요한 문제입니다.
일단 올바른 인과관계 다이어그램이 있으면 데이터를 보지 않아도 교란의 여부를 파악할 수 있습니다. 여기에 더해 두 가지 교란 해소 규칙인 ‘분리 인과 기준(DCC, disjunctive cause criterion)’과 ‘백도어 기준(BC, backdoor criterion)’을 상황에 따라 선택하여 교란을 해소할 수 있습니다.
인과관계 다이어그램의 개념적 분리

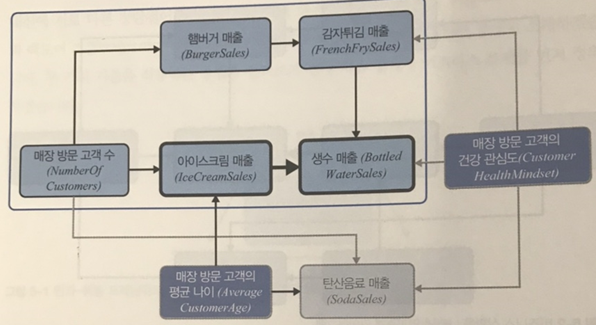
예시에서는 ‘아이스크림 매출’이 ‘생수 매출’에 미치는 영향(편향되지 않은 추정치)을 구하고자 합니다. 이 다이어그램은 교란변수가 어디에 숨은지 명확하게 보기 어렵기 때문에 좀 더 관리하기 쉬운 단위로 나눠볼 수 있습니다.

첫 번째 영역은 고객 수를 기반으로 아이스크림 매출과 햄버거, 감자튀김 매출 사이에 연결되는 관계를 보여줍니다. 두 번째 영역은 ‘매장 방문 고객의 평균 나이’와 ‘매장 방문 고객의 건강 관심도’의 영향을 보여줍니다.
1. 분리 인과 기준(DCC, disjunctive cause criterion)
분리 인과 기준 정의는 다음과 같습니다.
- 관심 변수 사이의 매개변수를 제외
- 두 관심 변수 중 하나 또는 두 관심 변수 모두의 직접적인 원인이 되는 모든 변수를 회귀에 추가
분리 인과 기준은 충분조건이지만 필요조건은 아닙니다. 즉 필요한 것 이상의 해소 방법을 적용하는 일종의 확장 규칙입니다. 하지만 그만큼 중복의 가능성이 있고 더 많은 데이터를 필요로 한다는 트레이드오프가 있습니다.
1-1. 분리 인과 기준 - 첫 번째 영역

(1) 하나 혹은 두 관심 변수 모두의 직접적인 요인인 모든 변수
첫 번째 영역에서 ‘매장 방문 고객 수’는 관심 변수인 ‘아이스크림 매출’의 직접적인 요인이므로 포함되어야 합니다. 또 ‘감자튀김 매출’도 관심 변수인 ‘생수 매출’의 직접적인 요인이므로 포함되어야 합니다. 그리고 ‘아이스크림 매출’과 ‘생수 매출’의 공통 요인은 없으므로 여기서는 생략합니다.
이때 ‘매장 방문 고객 수’ > ‘햄버거 매출’ > ‘감자튀김 매출’ > ‘생수 매출’ 의 사슬을 축소하고 위의 그림처럼 ‘매장 방문 고객 수’를 ‘생수 매출’의 직접적인 원인으로 취급할 수도 있습니다. 그러나 이렇게 하면 ‘매장 방문 고객 수’는 두 관심 변수의 공통된 직접적인 원인이 되기 때문에 교란 변수가 됩니다.
(2) 관심 변수 사이의 매개변수 제외
‘아이스크림 매출’과 ‘생수 매출’ 사이에는 매개변수가 없으므로 여기서는 제외 작업이 필요하지 않습니다.
(3) 교란 해소 확인
위의 (1)과 (2)의 과정을 거치고 두 관심 변수 사이에 교란 변수가 없는지 확인합니다. 여기서는 교란되지 않는 것을 확인할 수 있습니다.
1-2. 분리 인과 기준 - 두 번째 영역

두 번째 영역에서 관심 변수(아이스크림 매출 혹은 생수 매출)를 제외하고 데이터가 있는(연한 파란색 박스) 유일한 변수는 ‘탄산음료 매출’입니다. 이것은 관심 변수의 직접적인 요인이 아니기 때문에 DCC는 이 변수를 회귀에 포함하지 않습니다. 그러나 ‘고객 평균 나이’와 ‘고객의 건강 관심도’는 관심 변수에 대한 직접적인 요인이기 때문에 포함되어야 합니다. 하지만 이 두 변수는 데이터가 없기 때문에 실제로 사용하기 어렵습니다.
2. 백도어 기준 (BC, backdoor criterion)
이 방법은 교란 해소를 위한 필요조건이자 충분조건입니다. 이해하기 훨씬 더 복잡하고 완전히 정확한 인과관계 다이어그램이 필요하지만 실제 교란변수에 초점을 맞추고 회귀에 중복된 변수를 포함할 필요가 없습니다.
- 관심 요인(주의. 관심 효과 변수 아님)으로 가는 화살표를 가진 변수 찾기
- 해당 변수를 포함하는 모든 경로 찾기
- 그 경로가 ‘비인과적 경로’이면, 즉 경로에 분기나 충돌이 있으면 인과관계가 교란됨.
- 따라서 교란을 해소하기 위해 비인과적 경로를 차단(=통제)해야 함.
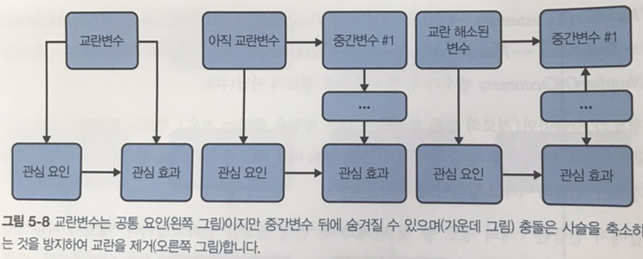
교란의 궁극적인 근본 원인은 공통 요인(아래 그림에서 왼쪽)입니다. 가운데 그림처럼 중간 변수 뒤에 숨겨질 수 있으며, 이때는 아직 교란이 해소되기 전인 상태입니다. 오른쪽 그림처럼 교란 변수와 중간 변수, 그리고 관심 효과 사이에 ‘충돌’이 있는 경우에 교란은 해소됩니다.
2-1. 백도어 기준 - 첫 번째 영역
첫 번째 영역에서 관심 요인은 ‘아이스크림 매출’입니다. 관심 요인으로 가는 화살표는 ‘매장 방문 고객 수’가 유일합니다. ‘매장 방문 고객 수’를 포함한 경로는 한 가지입니다.
아이스크림 매출 < 매장 방문 고객 수 > 햄버거 매출 > 감자튀김 매출 > 생수 매출
두 관심 변수인 ‘아이스크림 매출’과 ‘생수 매출’은 ‘매장 방문 고객 수’를 기준으로 분리됩니다. 따라서 ‘비인과적 경로’입니다. 그리고 이 경로상에서 충돌이 없기 때문에 이 경로는 관심 관계를 교란시키는 경로입니다.
교란 변수를 통제하기 위해서는 회귀에 비충돌 변수 중 하나를 포함하여 경로를 통제해야 합니다. 즉, 백도어 기준에 따라 ‘고객 수’, ‘햄버거 매출’, ‘감자튀김 매출’ 중 하나를 회귀에 포함하면 해당 경로를 충분히 통제할 수 있습니다. 그리고 선택하는 변수는 경험적으로 경로의 첫 번째 변수, 즉 관심 요인의 요인을 포함하는 것을 추천합니다. 예시에서는 ‘고객 수’를 선택한다면 해당 변수로 시작하는 다른 교란 경로도 자동으로 통제할 수 있게 됩니다.
2-2. 백도어 기준 - 두 번째 영역
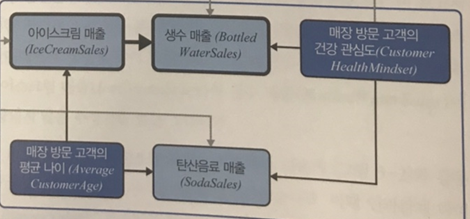
관심 요인인 ‘아이스크림 매출’의 영향 요인은 ‘고객 평균 나이’입니다. 경로는 아래와 같습니다.
아이스크림 매출 < 고객 평균 나이 > 탄산음료 매출 < 고객의 건강 관심도 > 생수 매출
두 관심 변수인 ‘아이스크림 매출’과 ‘생수 매출’ 사이에 분기와 충돌이 있습니다. 사슬이 아니므로 비인과적 경로입니다. 또 ‘탄산음료 매출’을 기준으로 충돌이 있기 때문에 경로가 차단된 상태입니다. 따라서 이 경로는 교란되지 않은 상태이고 통제할 필요가 없습니다. 결론적으로 데이터가 있는 변수인 ‘탄산음료 매출’은 회귀에 포함하지 않아도 됩니다.
<행동 데이터 분석> 책을 읽고 주요 내용과 제 생각을 정리한 글입니다.

Part 2 인과관계 다이어그램과 교란 해소
Chapter 5 인과관계 다이어그램을 통한 데이터 분석의 교란 해소
'데이터 분석 > Analytics' 카테고리의 다른 글
| [행동데이터분석] 부트스트랩을 활용한 불확실성 측정 (1) | 2024.01.05 |
|---|---|
| [행동데이터분석] 결측 데이터 처리 (0) | 2024.01.03 |
| [행동데이터분석] 인과관계 다이어그램 그리기 - (2) 변수 검증/확장/단순화 (0) | 2023.12.28 |
| [행동데이터분석] 인과관계 다이어그램 그리기 - (1) 변수 식별 (1) | 2023.12.28 |
| [행동데이터분석] 인과관계 다이어그램 (1) | 2023.12.21 |




댓글