앞에서 우리는 비즈니스에서 ‘관심을 보여야 하는 숫자(outcome)’와 그것을 표현하는 대표적인 방법인 ‘평균’에 대해서 알아봤습니다.
'평균'은 물론 데이터를 이해하는 데 중요한 값이지만, 현상 파악을 위해서, 보다 명확한 인과관계 통찰을 위해서는 다른 대푯값에 대한 이해도 필요합니다. 오늘은 데이터의 퍼짐 정도, 즉 데이터의 불규칙성을 표현하는 다른 대푯값인 ‘분산’과 ‘표준편차’에 대한 내용을 정리해볼게요.
'분산'으로 데이터의 펼쳐진 정도 확인하기
평균이 도출된 방법을 다시 한번 살펴보겠습니다. 평균값은 그것을 참값이라고 가정했을 경우 실제 데이터에 포함되는 '참값'에서 벗어난 값'을 최소화하는 값입니다. 정확하게는 '참값에서 벗어난 값의 제곱합'을 의미합니다. 예를 들어 어떤 서비스에 대한 만족도를 10점 만점으로 평가받았을 때 다음과 같은 결과를 얻었습니다.
| 응답자 | 만족도 | 평균과의 차이 | 평균과의 차이의 제곱 |
| A | 2 | -5 | 25 |
| B | 9 | +2 | 4 |
| C | 10 | +3 | 9 |
| 평균 | 7 | - | - |
평균에서 벗어난 값의 제곱을 모두 합하면 25+4+9=38 이라는 값이 얻어집니다. 다만, 이런 방식은 데이터의 수가 늘수록 합이 커지는 특징을 갖고 있습니다.
다음의 예를 살펴보겠습니다. 이번에는 40명에게 다른 서비스에 대한 만족도를 물었습니다. E1~E20까지 20명의 응답자는 6점을, F1~F20까지 20명의 응답자는 8점을 주었습니다. 이때 평균과의 차이의 제곱합은 1x40=40입니다.
| 응답자 | 만족도 | 평균과의 차이 | 평균과의 차이의 제곱 |
| E1 | 6 | -1 | 1 |
| E2 | 6 | -1 | 1 |
| ... | 6 | -1 | 1 |
| E20 | 6 | -1 | 1 |
| F1 | 8 | +1 | 1 |
| F2 | 8 | +1 | 1 |
| ... | 8 | +1 | 1 |
| F20 | 8 | +1 | 1 |
| 평균 | 7 | - | - |
처음 3명에게 만족도를 물었을 때 모두 평균값인 7점을 기준으로 2점 이상의 차이를 보였고, 다음에 20명에게 만족도를 물었을 때는 평균값에서의 차이가 모두 1점밖에 나지 않았습니다. '평균차이제곱합'을 통해 '나중에 평가한 서비스의 불규칙성이 더 크다'고 하기에는 조금 이치에 맞지 않는 것 같습니다. 그래서 나타난 개념이 '분산'입니다. '벗어난 값의 제곱합' 대신 '벗어난 값의 제곱 평균'을 사용한 것이 분산의 기본 개념입니다.
(통계학에서는 분산을 구할 때 벗어난 값의 제곱합을 사례수로 나누는 것이 아니라, '사례수-1'로 나눈 값을 사용합니다. 실제 모집단에서 일부의 표본을 추출하여 분산을 구하게 되면 그 기댓값이 모집단의 분산과는 차이(불편성)가 발생하기 때문에 이렇게 보정하는 방식을 사용하는데요, 데이터의 수가 많아지면 그렇게 큰 의미는 없기 때문에 여기서 더 설명하지 않아도 될 것 같습니다.)
분산을 좀 더 이해하기 쉽게 표현한 '표준편차'
앞에서 3명에게 만족도를 물었을 때의 제곱평균값은 38/3=12.7 입니다. 하지만, 10점 만점인 평가 척도에서 12.7만큼 데이터가 퍼져있다는 것은 아무래도 쉽게 이해하기 어렵습니다. 그러므로 좀 더 이해하기 쉬운 형태로 분산을 처리할 필요가 있었고, 이것을 제곱근(√)을 통해 해결한 것이 '표준편차'(Standard Deviation, SD)입니다. 12.7의 제곱근은 3.6 입니다. 만족도 점수와 평균과의 차이는 -5~+3 였으니 평균에서 벗어난 정도를 3.6 이라고 보는 것이 확실히 더 이해하기 쉽습니다.
표준편차를 어떻게 활용할 수 있을까?
표준편차는 다음과 같은 특징을 갖습니다.
- 데이터의 불규칙성이 어떠하든 '평균값 - 2 x SD(표준편차의 2배)' ~ '평균값 + 2 x SD'에 전체 데이터의 4분의 3 이상이 존재
- 정규분포를 따르는 데이터라면 '평균값 ± 1.96*SD'의 범위에 95%의 데이터가 존재
따라서 평균과 표준편차가 제시되어 있다면 데이터의 대략적인 모습을 파악할 수 있습니다.
정규분포다운 불규칙성이 내포되어 있든 아니든
"대체로 '평균값 ± 2 x SD' 의 범위 부근에 데이터가 존재한다"고 생각하면 된다
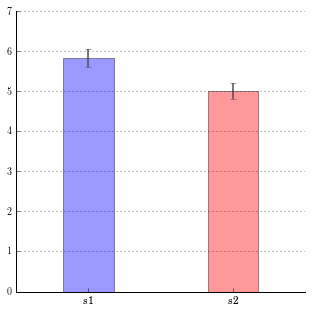
표준편차를 이해했다면 이제 아래와 같은 형태의 막대그래프를 읽는 것이 가능해집니다. 각 막대그래프는 어떤 데이터의 '평균'을 의미하고, 각 막대의 상단 중심에서 위아래로 그어진 선은 '±2SD(정확하게는 1.96SD)'의 범위를 나타냅니다. 이 범위를 '신뢰구간'이라고 합니다. 임의의 서로 다른 조건의 두 그룹에서 어떤 결과가 주어졌을 때, 그림에서 보는 것처럼 '평균값 ± 2SD' 라는 범위가 그룹 간에 겹치는 일이 없다는 것은 한 그룹의 '대략적으로 데이터가 존재하는 범위'에 다른 그룹의 데이터가 존재하는 것은 '당연한 일이 아니라'라는 의미입니다. 이때 두 그룹의 조건 차이가 결과에 영향을 미치지 않았는지 의심해 볼 만한 여지가 생깁니다.
오늘은 분산과 표준편차를 통해 점이 아닌, 구간으로 데이터를 바라보는 방법에 대해 다뤄보았습니다. 이후에는 데이터의 불규칙성에 대한 이야기, 통계적인 유의차, 검정에 대한 이야기를 다뤄보도록 하겠습니다. 오늘도 긴 글 읽어주셔서 감사합니다. 😄
이 글은 <통계의 힘: 실무활용 편 (니시우치히로무 지음)> 을 읽고, 책의 내용 일부와 저의 생각을 담아 적었습니다.
'데이터 분석 > Statistics' 카테고리의 다른 글
| 통계적 가설검정이 유용한 이유 (0) | 2022.01.13 |
|---|---|
| 통계적 검정에 앞서, '표준오차' 개념 이해하기 (0) | 2022.01.11 |
| '평균'이 '중앙값', '최빈값'보다 유용한 이유 (0) | 2021.12.29 |
| 비즈니스에서 가치 있는 데이터 분석 (0) | 2021.12.24 |
| 데이터를 '단 하나의 값'으로 이해하려는 성향 - 평균의 함정과 심슨의 역설 (0) | 2021.12.23 |




댓글